選択した画像 odds vs risk statistics 128256-What is the difference between odds and chances
Lastly, we have to take into account that odds (unlike risks) are rather difficult to understand, particularly for readers that are not particularly trained in statistics The risk of an event is a very simple concept it is the ratio between the number of subjects who experience the event and the total number of subjects at riskCalculation of probability (risk) vs odds In statistics, odds are an expression of relative probabilities, generally quoted as the odds in favor The odds (in favor) of an event or a proposition is the ratio of the probability that the event will happen to the probability that the event will not happenOdds Ratio (OR) measures the association between an outcome and a treatment/exposure Or in other words, a comparison of an outcome given two different groups (exposure vs absence of exposure) OR is a comparison of two odds the odds of an outcome occurring given a treatment compared to the odds of the outcome occurring without the treatment

Odds Ratio Relative Risk Risk Difference Statistics Tutorial 30 Marinstatslectures Youtube
What is the difference between odds and chances
What is the difference between odds and chances- Explanation and demonstration with simulated data of the difference between relative risk ratios and odds ratios, and how to extract them from a generalized linear model This post tries to explain the difference between odds ratios and relative risk ratios;Englishwise, they are correct it is the odds and the odds are based on a ratio calculation It is not , however, the odds ratio that is talked about when results are reported The odds ratio when results are reported refers to the ratio of two odds or, if you prefer, the ratio of two odds ratios




Odds Ratios And Risk Ratios Youtube
The differences between odds and probability lies in their ranges and denominators Ranges Odds are bound between 0 and positive infinity That is, you can have the odds of 0100 (not gonna happen), or (10thousand times more likely to happen than not) There are no negative odds Probability is bound between 0 and 1The relative risk is best estimated using a population sample, but if the rare disease assumption holds, the odds ratio is a good approximation to the relative risk — the odds is p / (1 − p), so when p moves towards zero, 1 − p moves towards 1, meaning that the odds approaches the risk, and the odds ratio approaches the relative risk 'Odds in favor' are odds describing the if an event will occur, while 'odds against' will describe if an event will not occur If you are familiar with gambling, 'odds against' are what Vegas gives as odds More on that later For the coin flip odds in favor of a HEADS outcome is 11, not 50% Visual Math
Odds ratios (OR) are commonly reported in the medical literature as the measure of association between exposure and outcome However, it is relative risk that people more intuitively understand as a measure of association Relative risk can be directly determined in a cohort study by calculating a rMedical Statistics – Measures of risk stats tutor community project wwwstatstutoracuk relative risk, the odds ratio is said to be significant if the confidence interval does not include 1 In this example the upper and lower limit of the 95% CI are both greater than 1 Risk Ratio vs Odds Ratio Whereas RR can be interpreted in a straightforward way, OR can not A RR of 3 means the risk of an outcome is increased threefold A RR of 05 means the risk is cut in half But an OR of 3 doesn't mean the risk is threefold;
Because in statistics odds are converted to the 'to one' standard we need to think about how we can consider the odds in favour of surviving which at present is none_death to deaths = 1 to nine = 19 = 1/9 = to convert this to the 'to one' standard we just divide each by the denominator (ie 9) so now we have the ratio ofRather the odds is Odds is the number having the outcome divided by the number not having the outcome The risk or odds ratio is the risk or odds in the exposed group divided by the risk or odds in the control group A risk or odds ratio = 1 indicates no difference between the groups
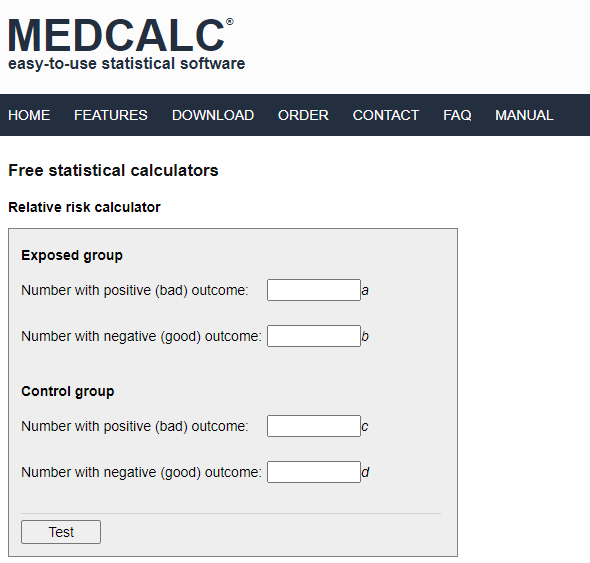



Medcalc S Relative Risk Calculator



Medical Statistics And Data Science Statistics
Odds and odds ratios rather than risk ratios are used in casecontrol studies because risks cannot be calculated However, odds and odds ratios can also used to display the results of cross sectional studies, cohort studies and randomized controlled trials The reason for this is that a commonly used regression model for binary (dichotomous) outcomes called logistic regression only allows the calculation of the odds The difference between odds ratio and risk ratio • ericminikel The other day I was emailing with a statistical genetics colleague about a rare SNP associated with a phenotype I stated that the minor allele frequency (MAF) was 07% in cases and 01% in controls, for a risk ratio of 7 After clicking send, I felt a twinge of regretThis implausible scenario is shown in Table 5, where collapsed counts for low (or high) risk subjects only produce a 2 × 2 table with an odds ratios of 400



Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau



R Calculate And Interpret Odds Ratio In Logistic Regression Stack Overflow
Conversely, probability lies between zero to one So, the closer the probability to zero, the more are the chances of its nonoccurrence and the closer it is to one, the higher are the chances of its occurrence Odds are the ratio of favourable events to the unfavourable eventThe odds ratio can also be used to determine whether a particular exposure is a risk factor for a particular outcome, and to compare the magnitude of various risk factors for that outcome OR=1 Exposure does not affect odds of outcome OR>1 Exposure associated with higher odds of outcome OR The math underlying odds and gambling can help determine whether a wager is worth pursuing The first thing to understand is that there are three distinct types of odds fractional, decimal, and



Training Cochrane Org Handbook Statistical Methods Revman5
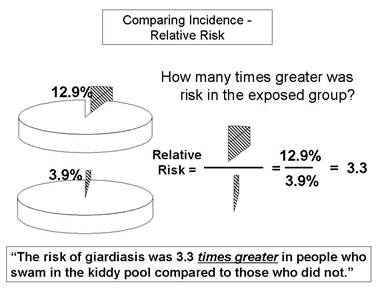



Relative Risk And Absolute Risk Definition And Examples Statistics How To
It is estimated as the difference in the absolute risk (of the event of interest) between persons exposed to the risk factor and persons not exposed to the risk factor It is usually expressed as a percentage Worked example Using the data in Table 1, the risk of sexual dysfunction attributable specifically to venlafaxine The odds ratio will estimate the average change in odds (the average odds ratio) among exposed individuals only when all individual odds ratios are equal and all individual outcome risks without exposure are equal 1;Absolute Risk Difference vs Relative Risk Reduction Absolute Risk Difference provides number needed to treat (NNT), so may be more helpful NNT=1/ARD If RRR is reported, multiply this with risk in control group (p 2) to get ARD RRR=ARD/p 2 ARD= RRR×p 2 16
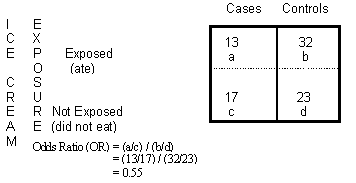



Odds Ratio Calculation And Interpretation Statistics How To




Odds Ratio Http Www Slideshare Net Terryshaneyfelt7 What Does An Odds Ratio Or Relative Risk Mean Statistics Math Research Methods Academic Research
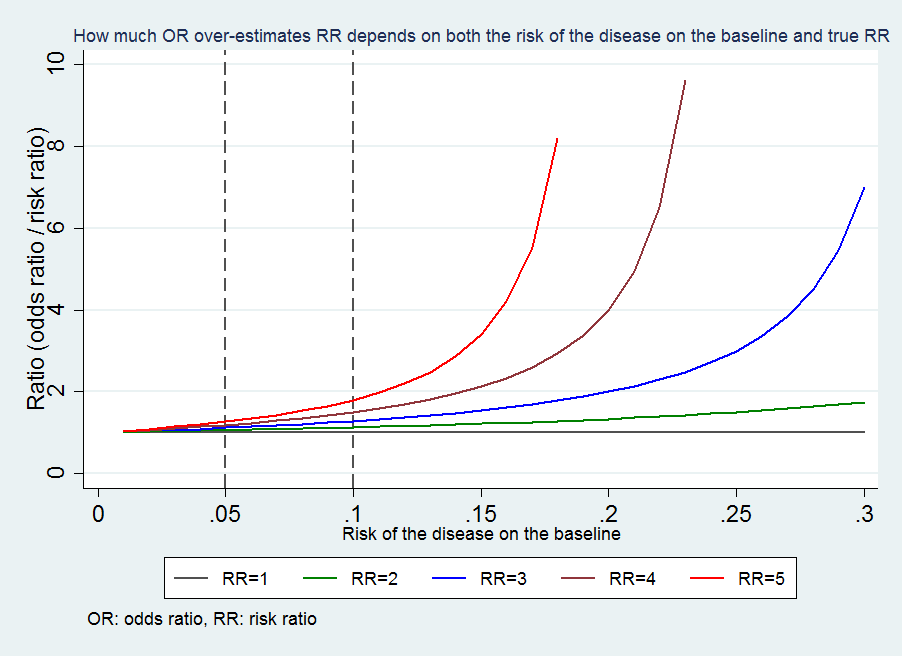
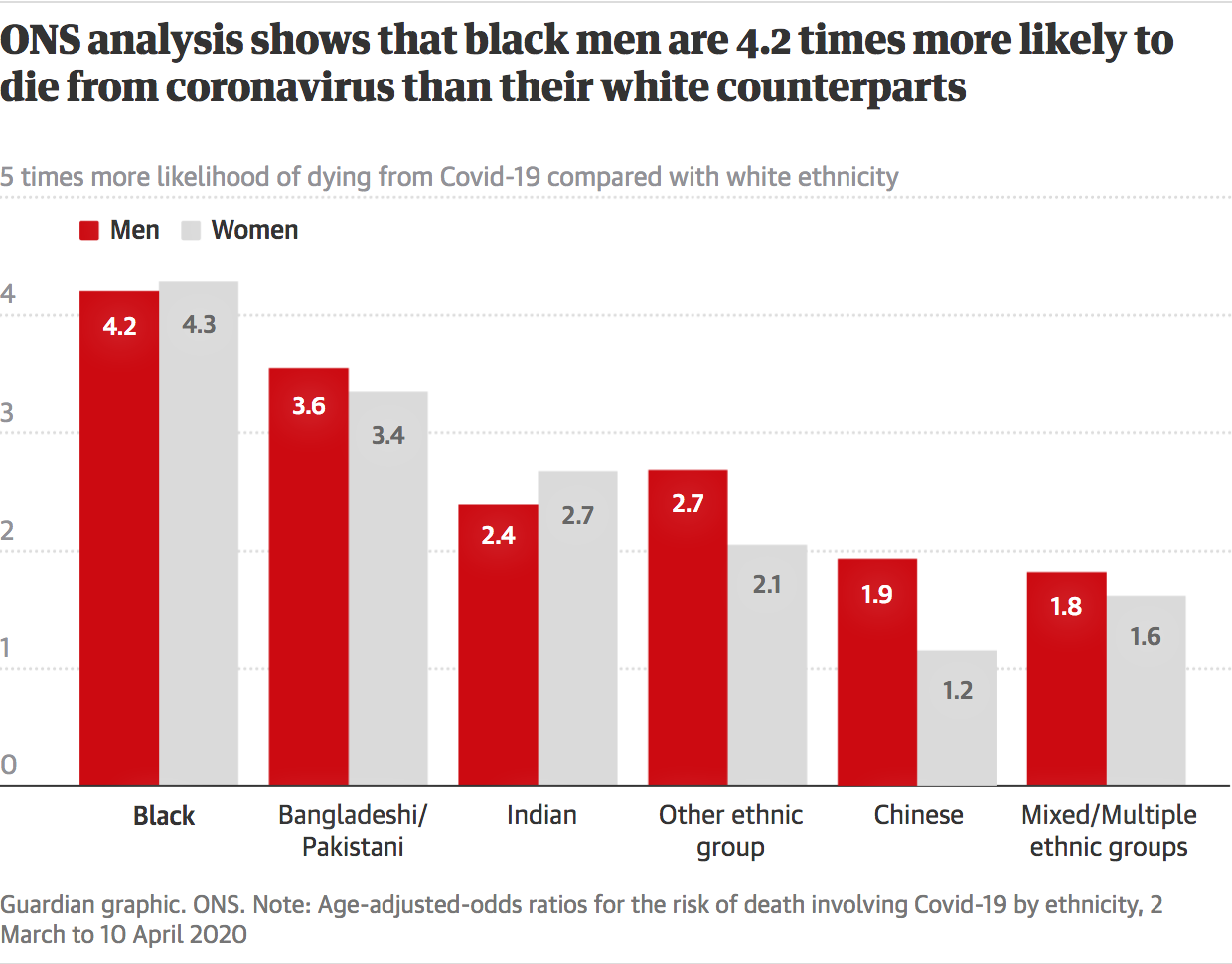
Odds ratio in this example is found to be hight () (P Note that an odds ratio is a good estimate of the risk ratio when the outcome occurs relatively infrequently (Diabetes, chronic respiratory diseases, hypertension, and cancer were all risk factors as well, as we see in the chart By comparison, the CFR was 09% – more than ten times lower – for those without a preexisting health condition Above we saw that the elderly are most at risk




Pdf Statistical Notes For Clinical Researchers Risk Difference Risk Ratio And Odds Ratio




Statistics 0 Lecture 7 Tuesday September 13 Ppt Download
Common pitfalls in statistical analysis Odds versus risk In biomedical research, we are often interested in quantifying the relationship between an exposure and an outcome "Odds" and "Risk" are the most common terms which are used as measures of association between variablesOdds Ratio, Relative Risk, and Risk Difference How to Use Odds Ratio, Relative Risk, and Risk Difference to Describe the Association Between Two Categorical The correct interpretation of an odds ratio is The patients who received standard care had an odds of dying 371 times more than patients treated with the new drug You must be clear that it is the odds of dying that are being compared Otherwise it is a risk ratio, which is not the same calculation But does it really matter?
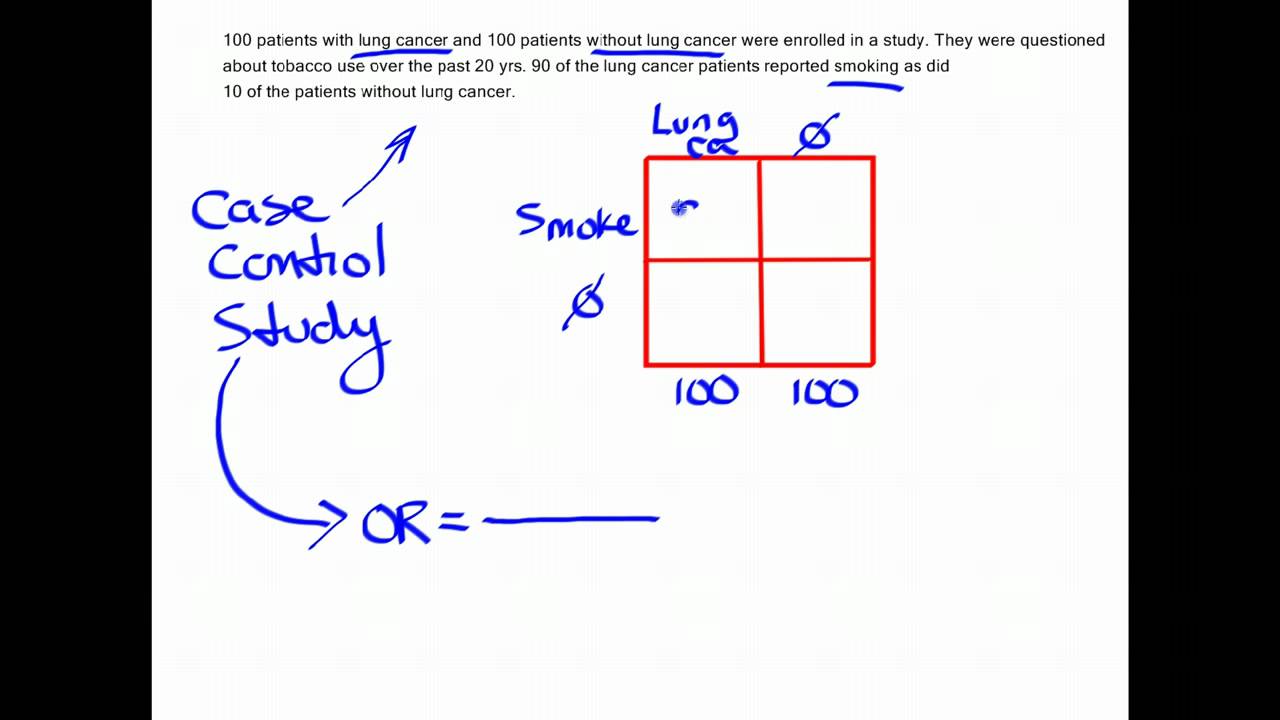



How To Calculate An Odds Ratio Youtube
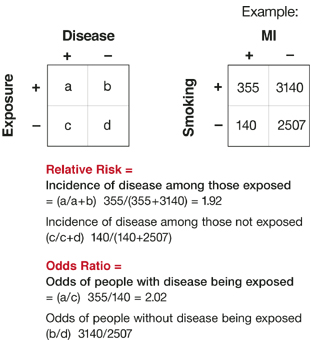



Relative Risks And Odds Ratios What S The Difference Mdedge Family Medicine
After converting the odds ratio to a risk ratio, the actual risk is 14 (mortality is 14 times more likely in patients with ICU delirium compared to those without ICU delirium) Because the incidence rate in the nondelirium group is high, the odds ratio exaggerates the true risk demonstrated in the study Odds Ratio is the odds that the diseased group was exposed, divided by odds that the nondiseased group was exposed (a/c)/(b/d) in the classic table Relative Risk is the risk of developing disease in the exposed/intervention group, that is to say the odds of disease in the intervention arm divided by the odds of disease in the placebo arm (which is what is describedRiskkvoter är lättare att uppfatta intuitivt än oddskvoter Om en behandlingsprövning ger RR 0,80 var risken i den behandlade gruppen 80 procent av risken i kontrollgruppen




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios
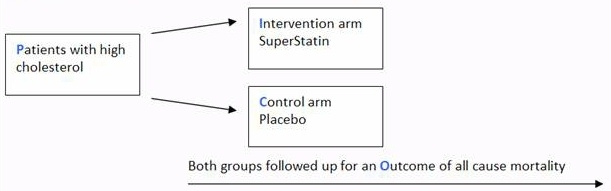



A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence
And how just a few letters in the code fitting a generalized linear model mean the difference betweenThe odds ratio (OR) is one of several statistics that have become increasingly important in clinical research and decisionmaking It is particularly useful because as an effectsize statistic, it gives clear and direct information to clinicians about which treatment approach has the best odds of benefiting the patient Odds ratio vs relative risk Odds ratios and relative risks are interpreted in much the same way and if and are much less than and then the odds ratio will be almost the same as the relative risk In some sense the relative risk is a more intuitive measure of effect size Note that the choice is only for prospective studies were the distinction




Odds Ratio Relative Risk Risk Difference Statistics Tutorial 30 Marinstatslectures Youtube



Q Tbn And9gcqsrft9mxr7dpz7nmjrd2rigdx Ivp6aahq2v9iti13quuix7yw Usqp Cau
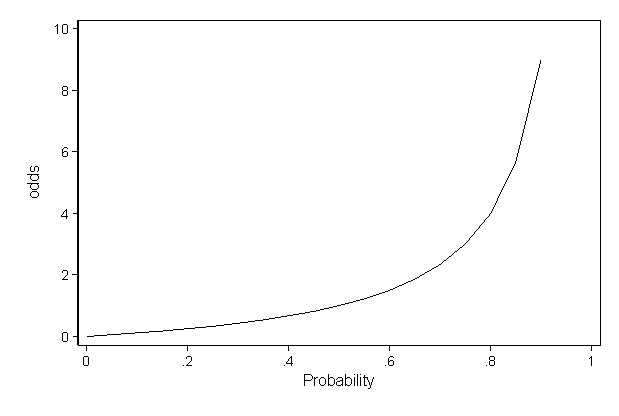
Odds of dying estimates assume that mortality trends change slowly over time with changes of only a few percentage points from year to year Currently, COVID19 trends are changing too rapidly to confidently anticipate future risk levels Visit the Injury Facts COVID19 page to track realtime data in the United States COVID19The risk of a child getting the flu is 45 % which can also be written as 045 Because we have the risk, we can use the second odds formula o d d s = r i s k 1 − r i s k = 045 1 − 045 = 045 055 = 0818 The odds of a child getting the flu is 0818 to 1 « Previous Risk ratios, odds ratios, and hazard ratios are three common, but often misused, statistical measures in clinical research In this paper, the authors dissect what each of these terms define, and provide examples from the medical literature to illustrate each of these statistical measures Finally, the correct and incorrect methods to use these measures are summarized




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1




Attributable Risk And Odds Ratio Online Medical Library
The more common the disease, the larger is the gap between odds ratio and relative risk In our example above, p wine and p no_wine were 0009 and 0012 respectively, so the odds ratio was a good approximation of the relative risk OR = 0752 and RR = 075 A difference between 0010 and 0001, when considering the risk that people suffer serious side effects, is more noteworthy than the difference between 0410 and 0401 7 Number needed to treat A related measure, based on the absolute risk reduction, is the number needed to treat (NNT), which is defined as the reciprocal of the absolute risk reductionIn general conversation the terms 'risk' and 'odds' are used interchangeably (as are the terms 'chance', 'probability' and 'likelihood') as if they describe the same quantity In statistics, however, risk and odds have particular meanings and are calculated in different ways




Rr Interpretation Http Www Slideshare Net Terryshaneyfelt7 What Does An Odds Ratio Or Relative Risk Mean Statistics Math Research Methods Nursing Research




Spss Video 10 Obtaining Odds Ratio Relative Risk In Spss Risk Lean Six Sigma Odds
The basic difference is that the odds ratio is a ratio of two odds (yep, it's that obvious) whereas the relative risk is a ratio of two probabilities (The relative risk Ratios of probabilities, they can be defined in two different ways odds in favor of an event ("odds on") or against an event A ("Odds Against) Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds Risk ratios can be misleading as to the importance of the difference when the risk in the comparison group is very small For example, if the risk in the unexposed group is 001 and the risk in the exposed group is 005, that leads to a risk ratio of 5, but a risk difference of only 004
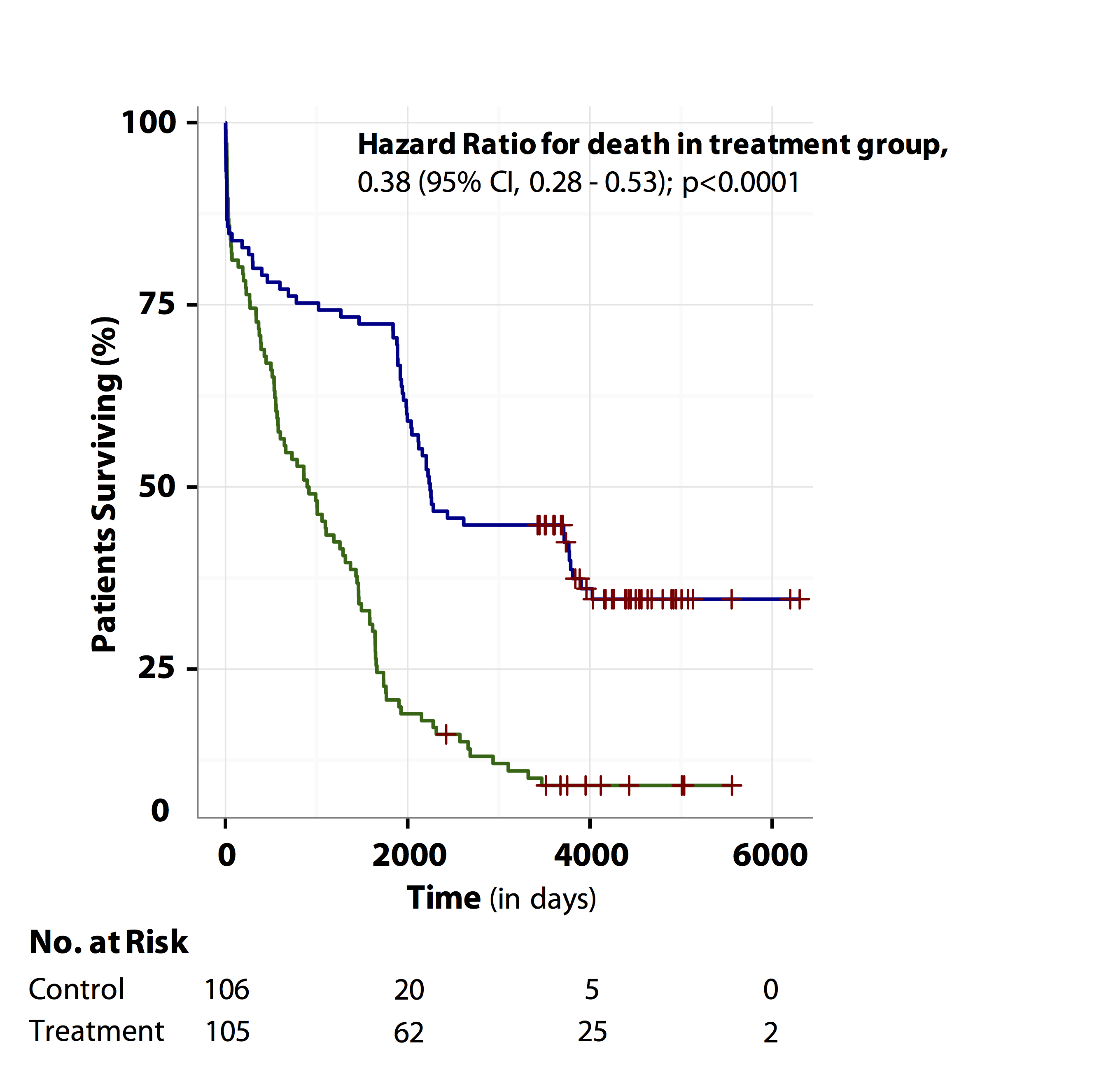



Tutorial About Hazard Ratios Students 4 Best Evidence




Odds Ratios And Risk Ratios Youtube
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Odds ratio (OR), risk ratio (RR), and prevalence ratio (PR) are some of the measures of association which are often reported in research studies quantifying the relationship between an independent variable and the outcome of interest There has been much debate on the issue of which measure is appropriate to report depending on the study design




Chapter 6 Choosing Effect Measures And Computing Estimates Of Effect Cochrane Training




Rde Restorative Dentistry Endodontics




The Binomial Applied Absolute And Relative Risks Chisquare




The Binomial Applied Absolute And Relative Risks Chisquare




Pdf Using Risk And Odds Ratios To Assess Effect Size For Meta Analysis Outcome Measures



Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau



Research Statistics Basics Contents 1 Basic Concepts 2 References Basic Concepts Null Hypothesis The Hypothesis That The Independent Variable Has No Effect On The Dependent Variable For Example Steroids Do Not Improve Outcomes In Ards Would Be
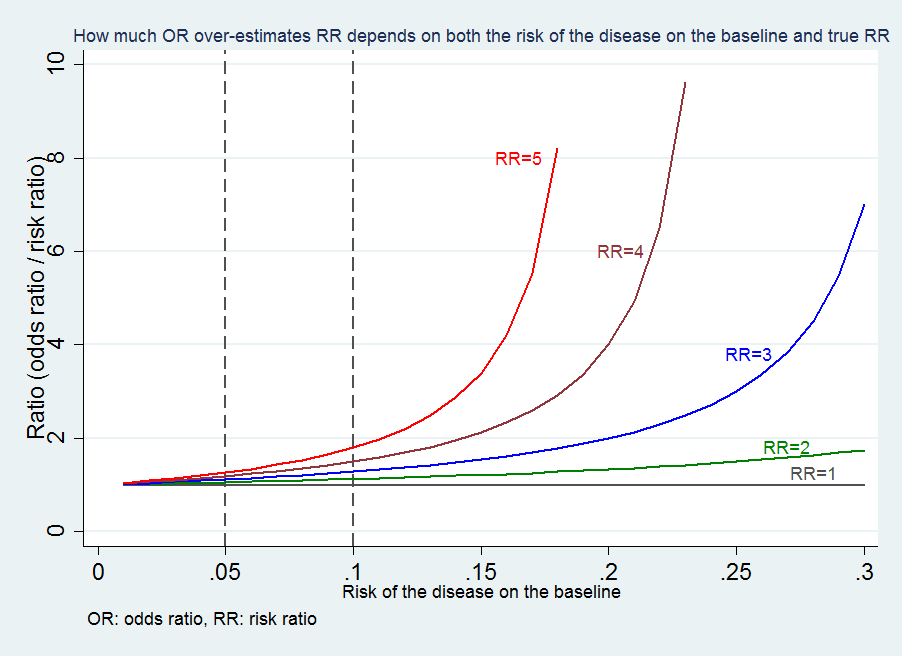



Medical Statistics And Data Science Statistics




Relative Risk Vs Odds Ratio Extensive Video Youtube




Odds Ratios Versus Relative Risk
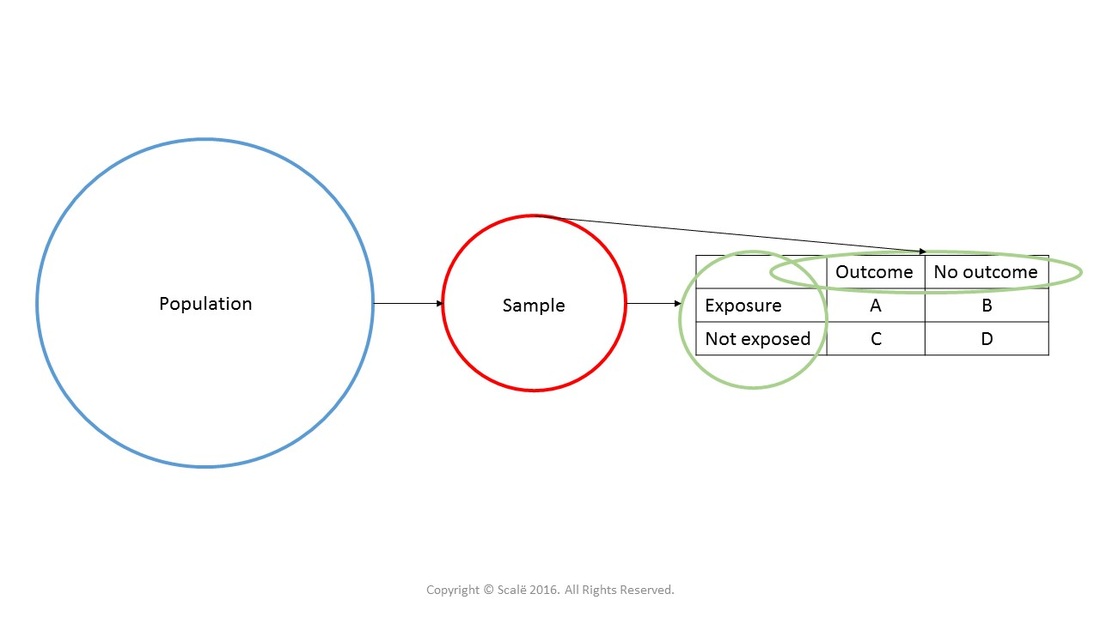



Calculate Relative Risk With 95 Confidence Intervals




A Odds Ratio With Corresponding 95 Confidence Intervals For Download Scientific Diagram
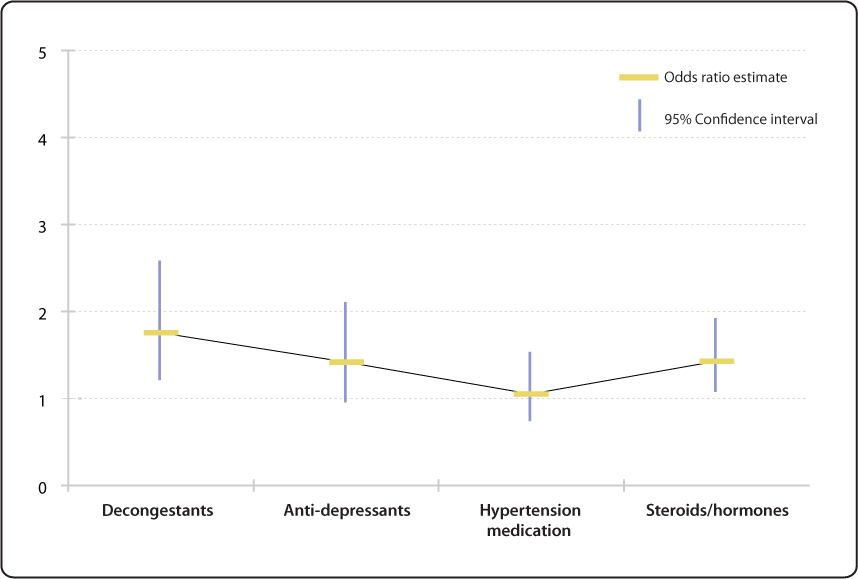



Relative Risk Odds Ratio Estimate With 95 Confidence Intervals For People To 66 Years Of Age With Current Medication Use Ever Having Voice Problems Or Disorders Nidcd




2 Descriptive Statistics And Unadjusted Odds Ratios For Risk Of Download Table



Ctspedia Ctspedia Oddsrisk




What Are The Odds Stats With Cats Blog
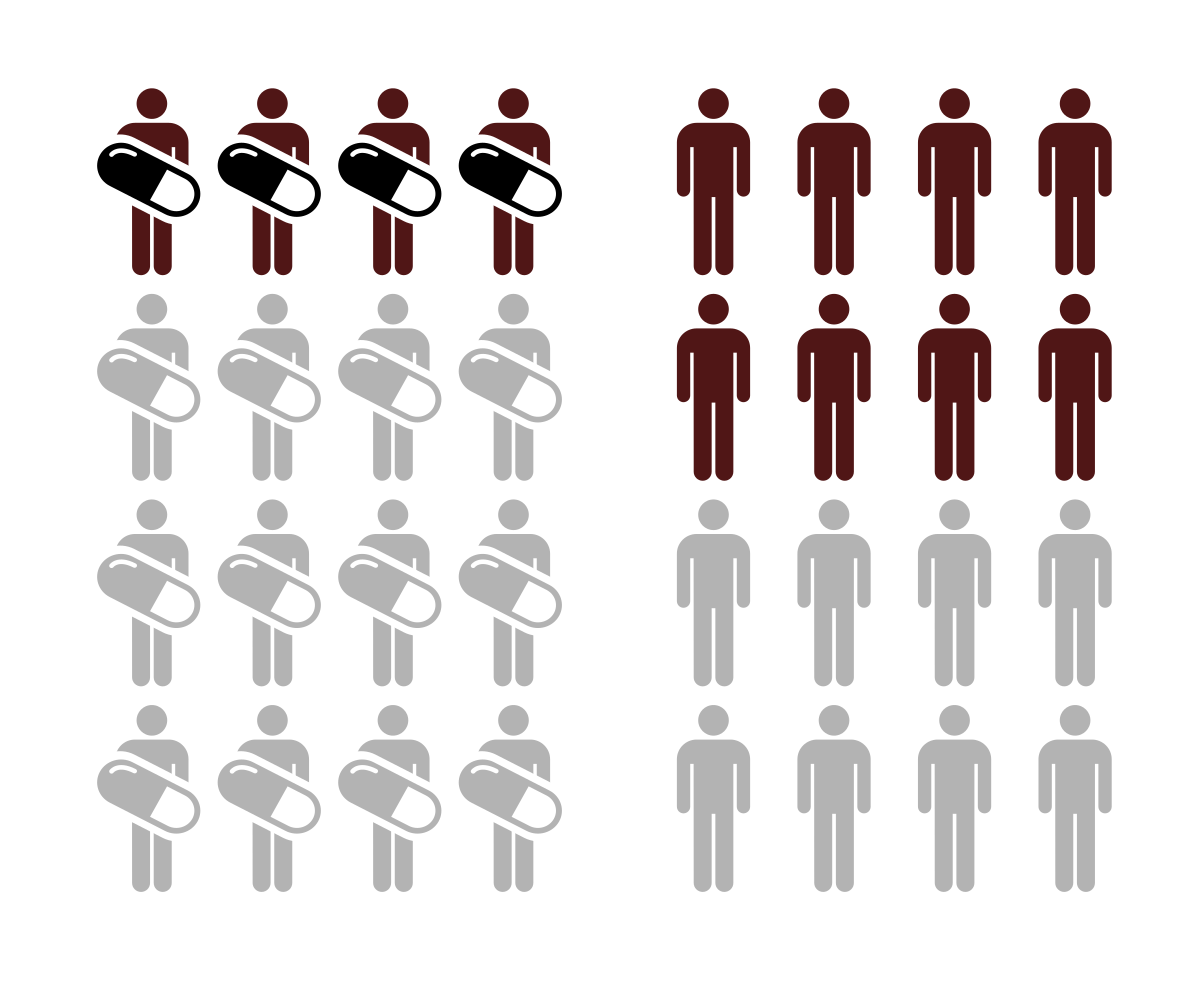



Relative Risk Wikipedia




Statistics Basics Odds Ratio And Relative Risk Calculation In Excel Bi Practice




What Is An Odds Ratio And How Do I Interpret It Critical Appraisal
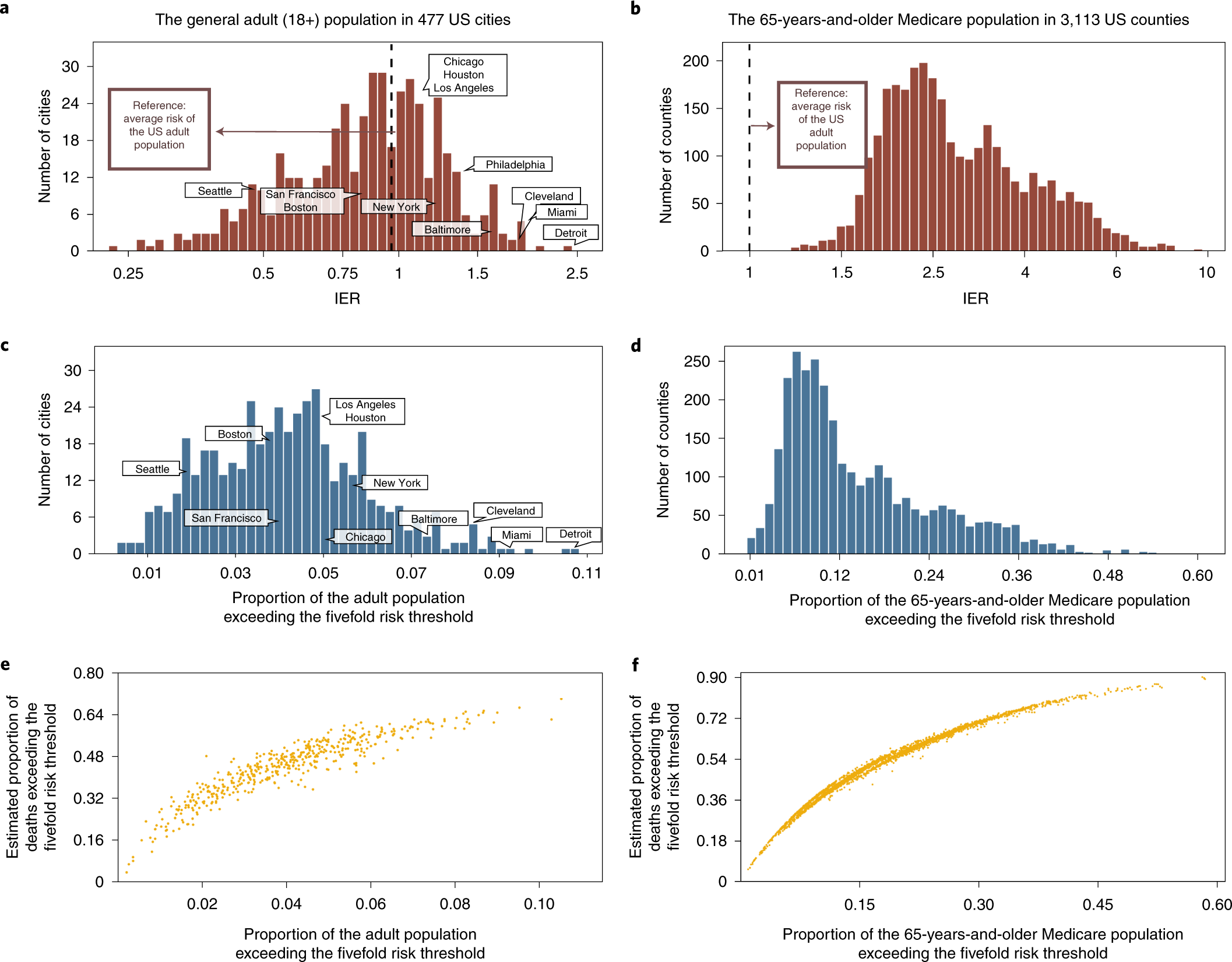



Individual And Community Level Risk For Covid 19 Mortality In The United States Nature Medicine




Odds Ratio Wikipedia




Medical Statistics Ix Bias Relative Risk And Odds Ratio



Full Article How Big Is A Big Odds Ratio Interpreting The Magnitudes Of Odds Ratios In Epidemiological Studies




Risk Of Being Killed By Police Use Of Force In The United States By Age Race Ethnicity And Sex Pnas




Interpreting Odds Ratio Senguptas Research Academy




Understanding Systematic Reviews And Meta Analysis Archives Of Disease In Childhood



Introduction To Genetic Epidemiology Lesson 5 Analyzing The Data



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1




The Difference Between Relative Risk And Odds Ratios The Analysis Factor
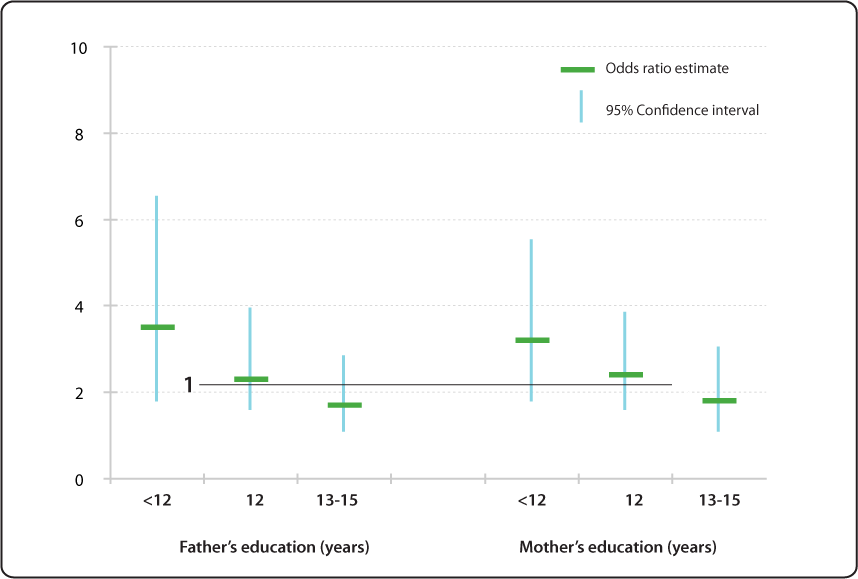



Relative Risk Odds Ratio Estimate With 95 Confidence Intervals Of Children Having Specific Language Impairment Sli By Parent S Level Of Education Reference College Graduate Or More Education 16 Years Nidcd
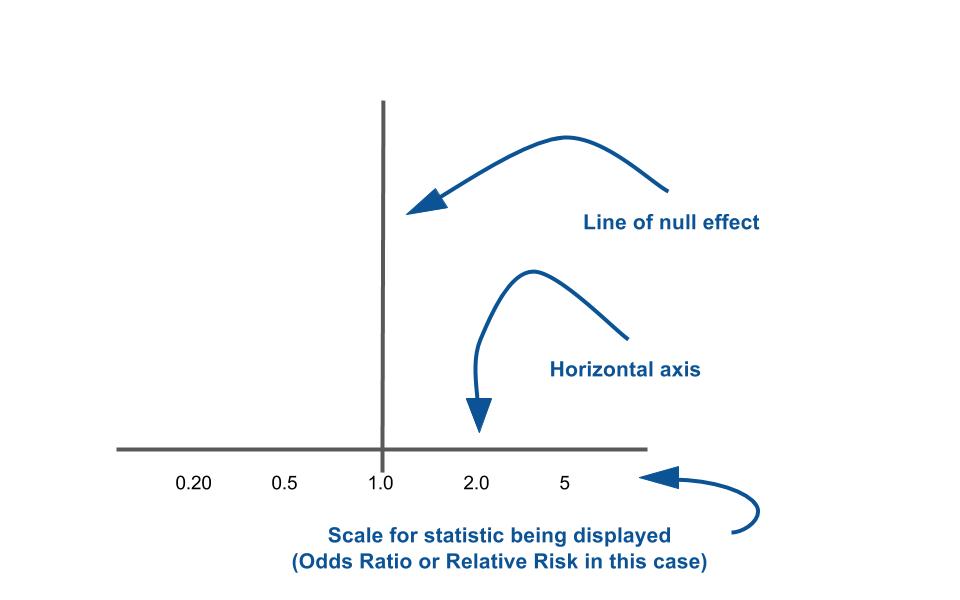



Tutorial How To Read A Forest Plot Students 4 Best Evidence



Http Www Floppybunny Org Robin Web Virtualclassroom Stats Basics Part13 Risks Rates Odds Pdf




Relative Risk Http Www Slideshare Net Terryshaneyfelt7 What Does An Odds Ratio Or Relative Risk Mean Study Skills Statistics Math Research Methods




Relative Risk Odds Ratios Youtube




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios




Odds Ratio Wikipedia
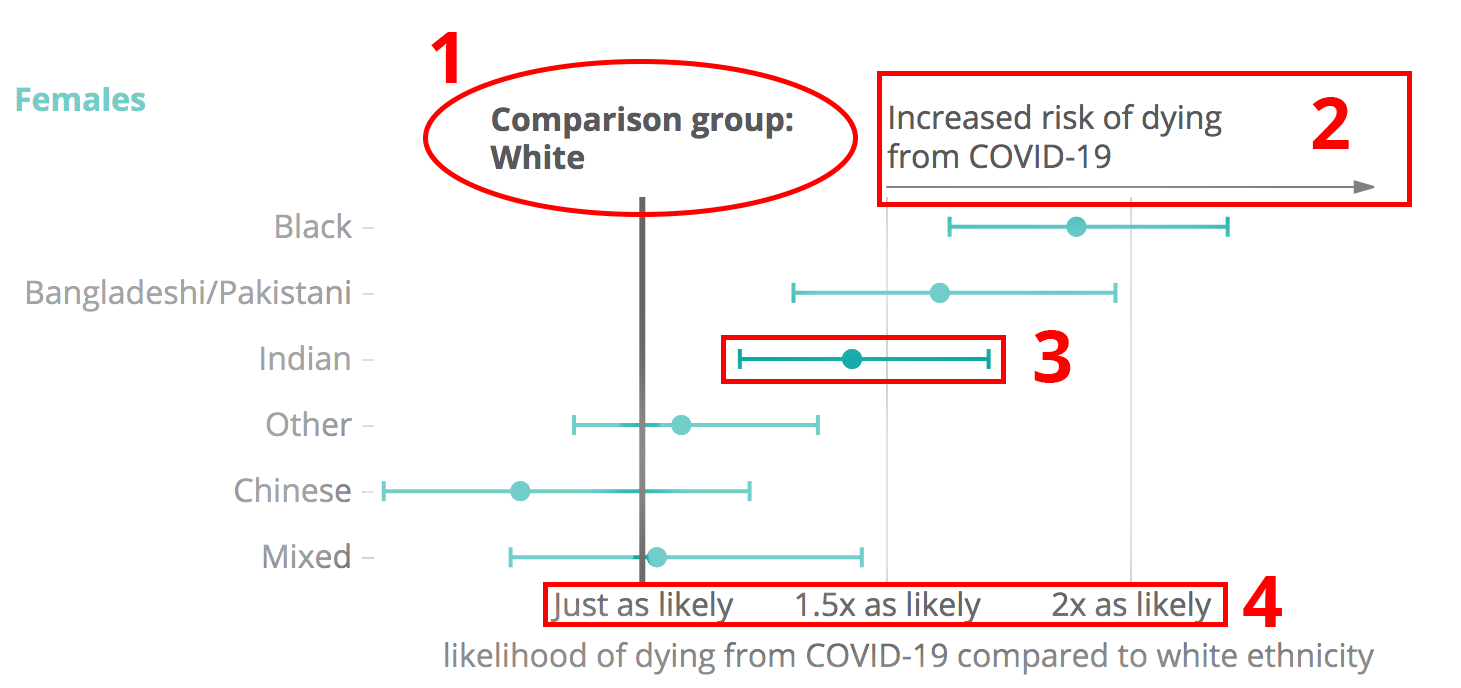



Against All Odds How To Visualise Odds Ratios To Non Expert Audiences Henry Lau




Pdf What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios




Forest Plot Showing Relative Statistics Of Odds Ratio A And B Or Download Scientific Diagram
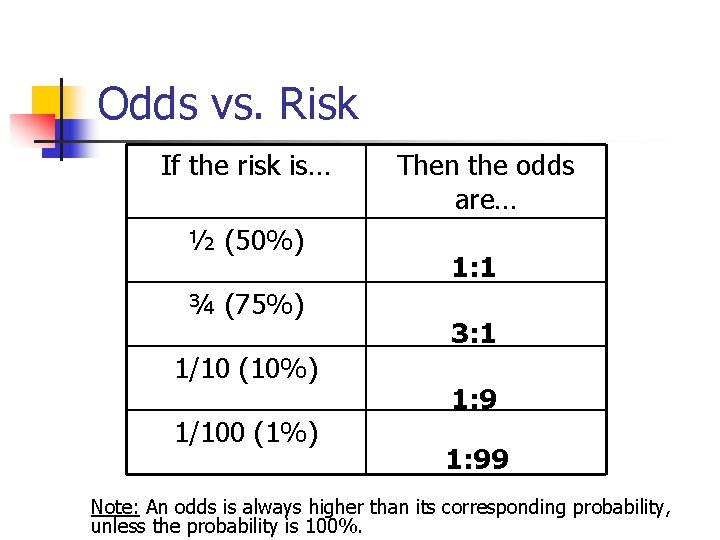



The Binomial Applied Absolute And Relative Risks Chisquare
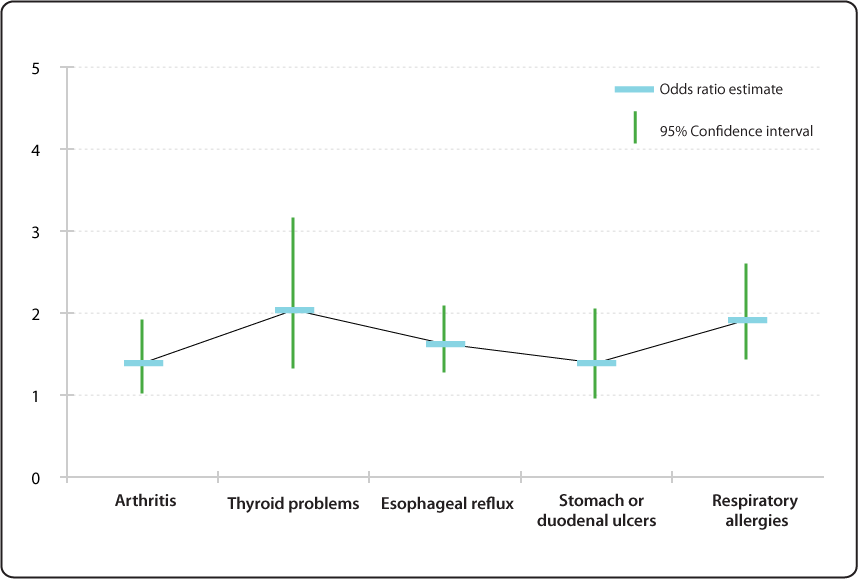



Relative Risk Odds Ratio Estimate With 95 Confidence Intervals For People To 66 Years Of Age And With Selected Conditions Ever Having Voice Problems Or Disorders Nidcd



How To Read A Forest Plot Cochrane Uk



Orr Objective Response Rate And Related Statistics Part 2 Odds Ratio
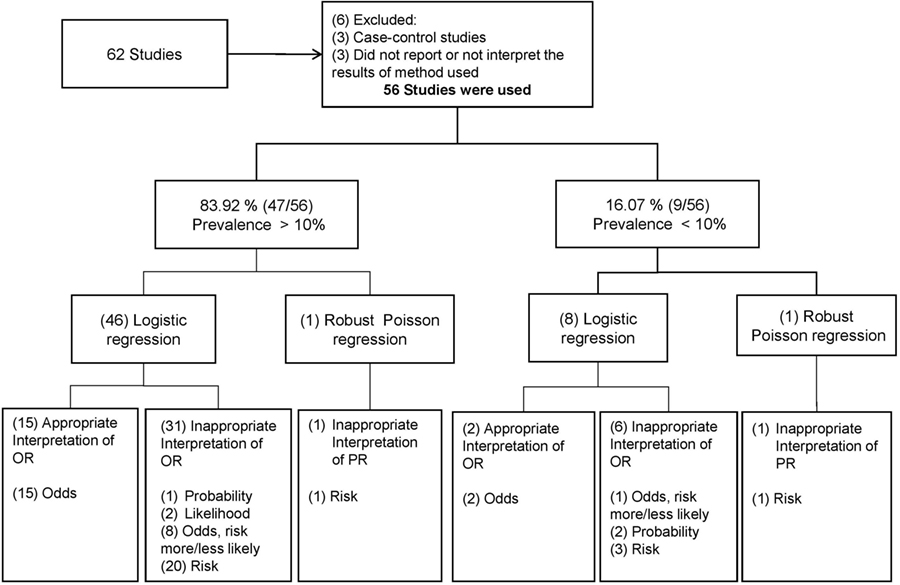



Frontiers Odds Ratio Or Prevalence Ratio An Overview Of Reported Statistical Methods And Appropriateness Of Interpretations In Cross Sectional Studies With Dichotomous Outcomes In Veterinary Medicine Veterinary Science




Odds Ratio Relative Risk Epidemiology Statistics Tutorial Student Evaluate Treatments Student Hippocratic Oath Tutorial
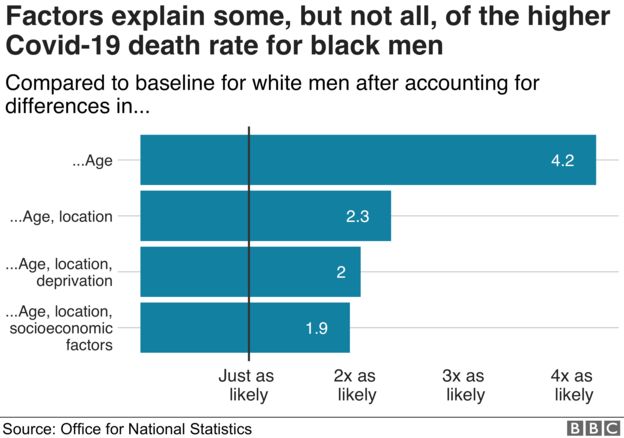



Against All Odds How To Visualise Odds Ratios To Non Expert Audiences Henry Lau
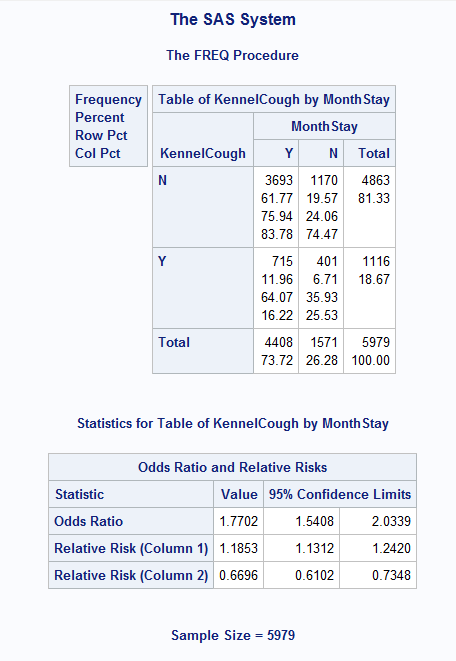



Different Odds Ratio From Proc Freq Proc Logisti Sas Support Communities
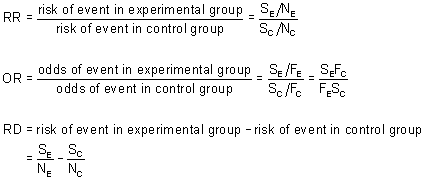



Box 9 2 A Calculation Of Rr Or And Rd




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1



Relative Risk Ratios And Odds Ratios




Look At Slide 25 In The Descriptive And Inferential Chegg Com



Odds Vs Risk Vantage Research



1




Statistics For Afp Dr Mohammad A Fallaha Afp




Statquest Odds Ratios And Log Odds Ratios Clearly Explained Youtube




Assessing Associations With A Categorical Outcome Sage Research Methods
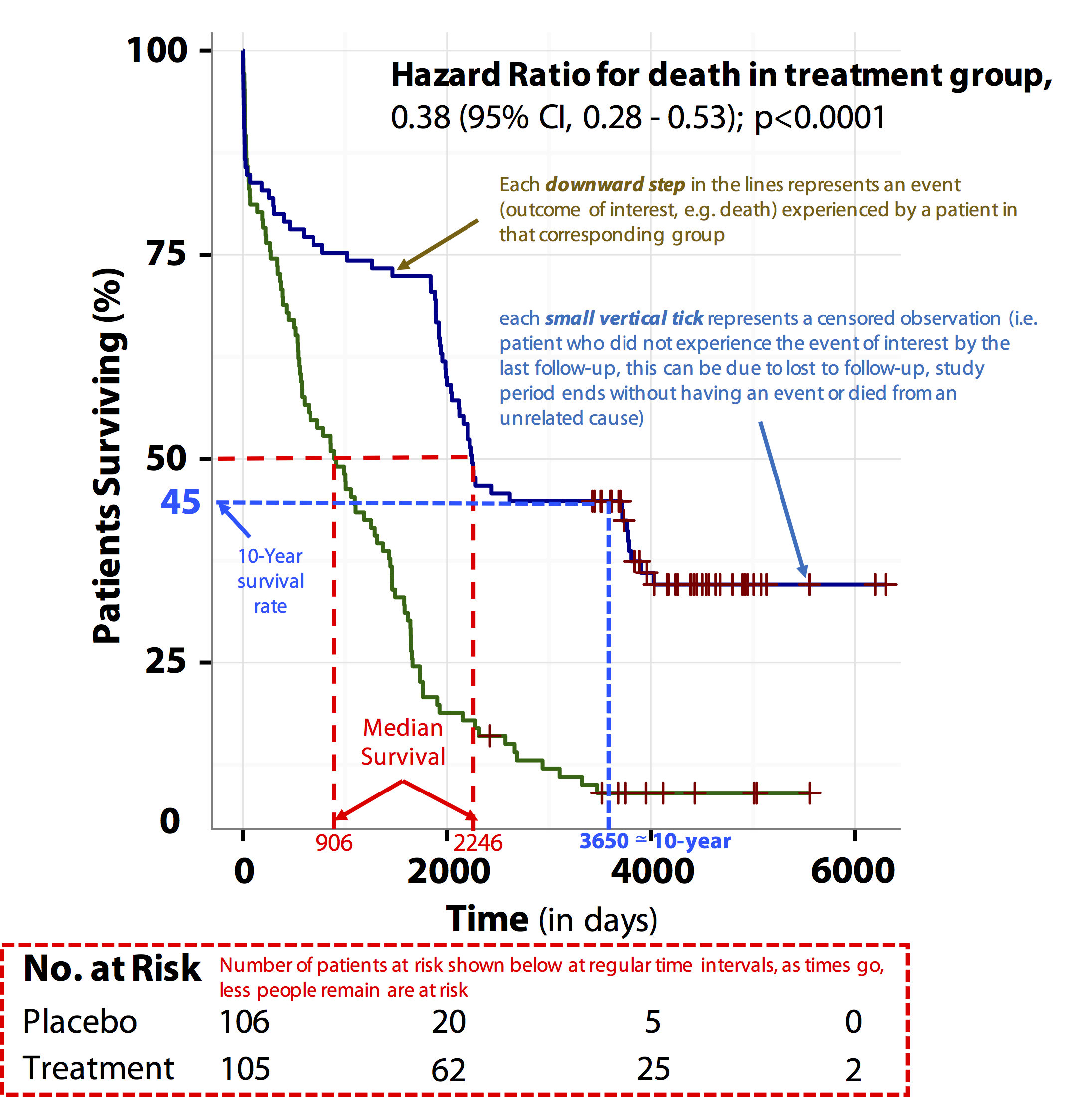



Tutorial About Hazard Ratios Students 4 Best Evidence
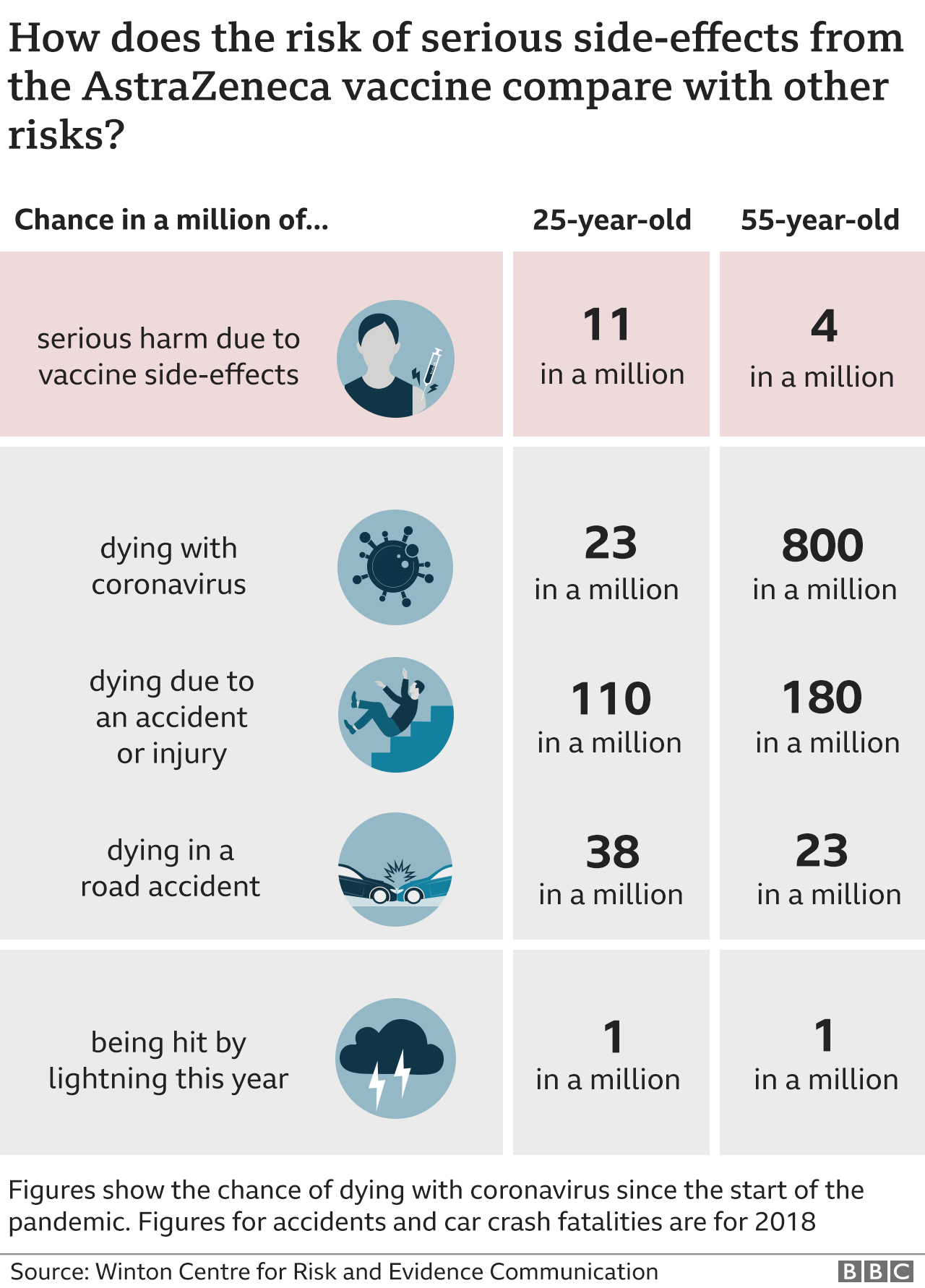



Astrazeneca Vaccine How Do You Weigh Up The Risks And Benefits c News
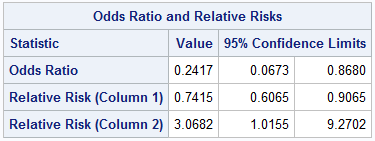



Statistics Basics Odds Ratio And Relative Risk Calculation In Excel Bi Practice




Statistical Forum
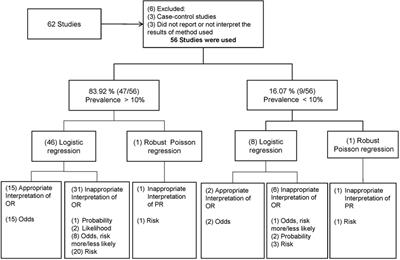



Frontiers Odds Ratio Or Prevalence Ratio An Overview Of Reported Statistical Methods And Appropriateness Of Interpretations In Cross Sectional Studies With Dichotomous Outcomes In Veterinary Medicine Veterinary Science
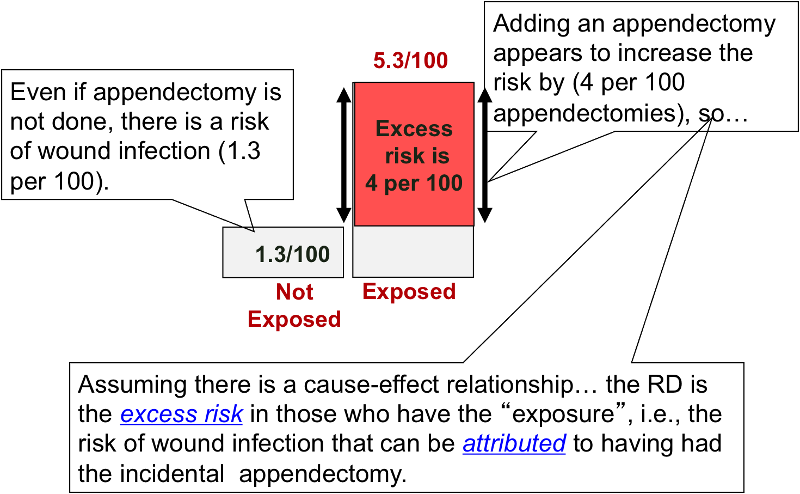



Risk Differences And Rate Differences



Against All Odds How To Visualise Odds Ratios To Non Expert Audiences Henry Lau




Bi Practice Page 4 A Journey Of A Thousand Miles Begins With The First Step




Calculate Relative Risk With 95 Confidence Intervals




Odds Ratio Wikipedia




What Is An Odds Ratio And How Do I Interpret It Critical Appraisal




Statistics In Medicine Calculating Confidence Intervals For Relative Risks Odds Ratios And Standardised Ratios And Rates The Bmj



A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence



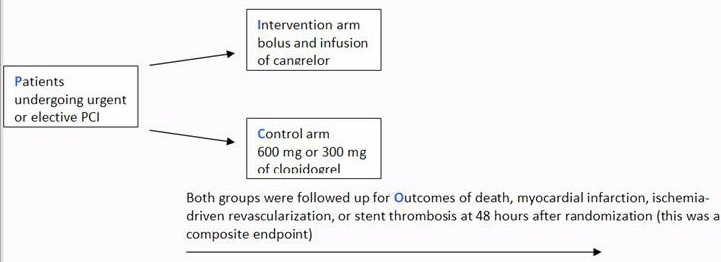
Faq How Do I Interpret Odds Ratios In Logistic Regression




Statistics Part 13 Measuring Association Between Categorical Data Relative Risk Odds Ratio Attributable Risk Logistic Regression Data Lab Bangladesh




Odds Ratio Relative Risk Risk Difference Statistics Tutorial 30 Marinstatslectures Youtube Study Skills Statistics Tutorial




Forest Plot Showing Relative Statistics Of Odds Ratio A And B Or Download Scientific Diagram
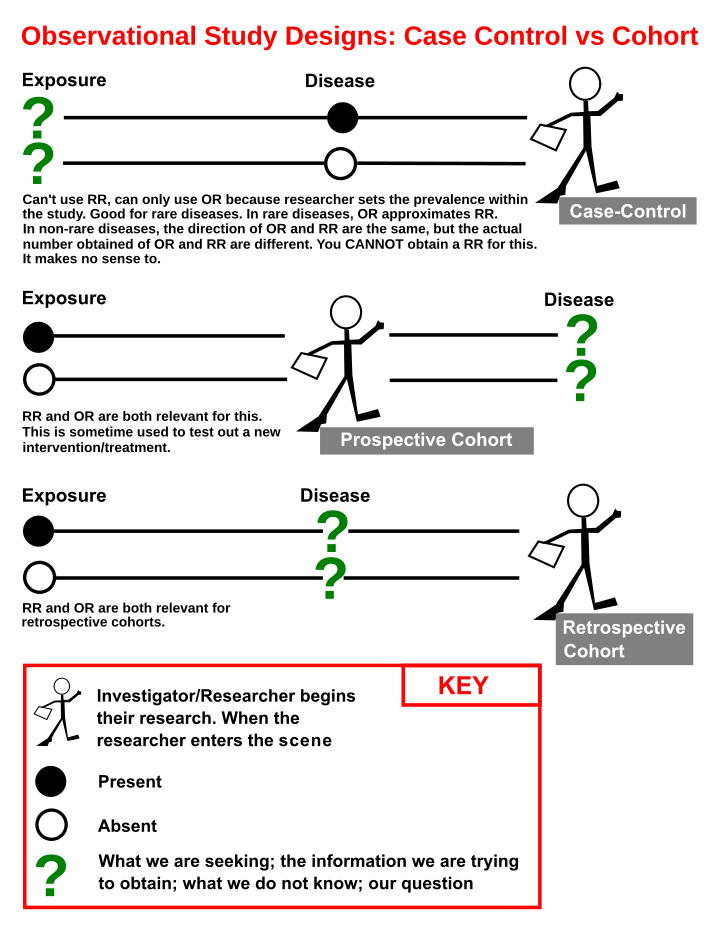



Cohort Statistics Wikiwand



Introduction To Genetic Epidemiology Lesson 5 Analyzing The Data
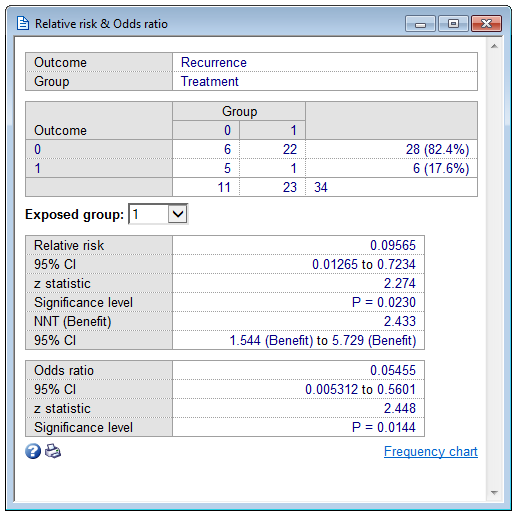



Relative Risk Odds Ratio




Solved Look At Slide 25 In The Descriptive And Inferentia Chegg Com




Pdf Common Pitfalls In Statistical Analysis Odds Versus Risk
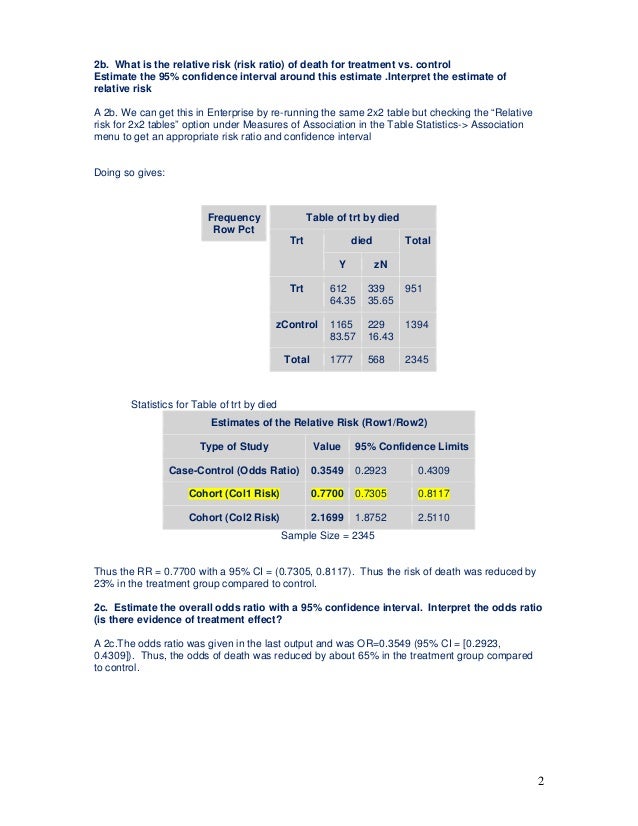



Testing Of Hypothesis Homework Help1
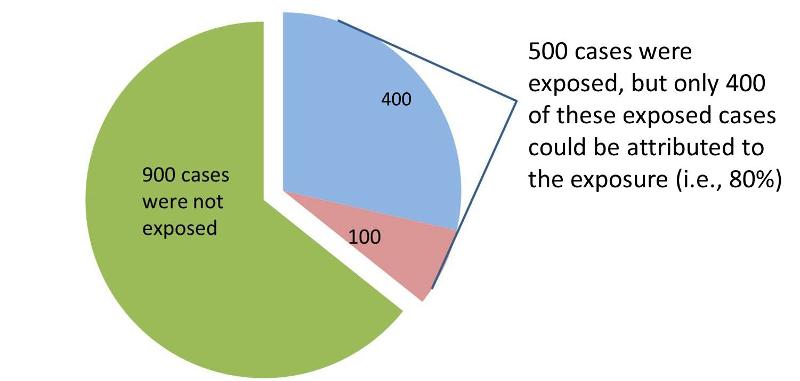



Measures Of Association




Medical Statistics Ix Bias Relative Risk And Odds Ratio Youtube
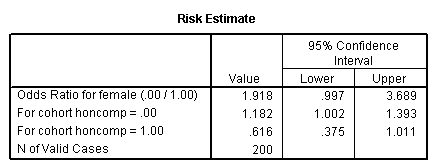



Logistic Regression Spss Annotated Output



コメント
コメントを投稿